Robust Symmetry Detection via Riemannian Langevin Dynamics

Jihyeon Je1*, Jiayi Liu1*, Guandao Yang1*, Boyang Deng1*, Shengqu Cai1, Gordon Wetzstein1, Or Litany2, Leonidas Guibas1
1Stanford University 2Technion
*Equal contribution
Paper arXiv Code Colab Demo
Teaser Image

In this work, we present a new perspective of understanding symmetries, which leads to the adoption of Riemannian Langevin dynamics to symmetry detection.

Abstract

Symmetries are ubiquitous across all kinds of objects, whether in nature or in man-made creations. While these symmetries may seem intuitive to the human eye, detecting them with a machine is nontrivial due to the vast search space. Classical geometry-based methods work by aggregating "votes" for each symmetry but struggle with noise. In contrast, learning-based methods may be more robust to noise, but often overlook partial symmetries due to the scarcity of annotated data. In this work, we address this challenge by proposing a novel symmetry detection method that marries classical symmetry detection techniques with recent advances in generative modeling. Specifically, we apply Langevin dynamics to a redefined symmetry space to enhance robustness against noise. We provide empirical results on a variety of shapes that suggest our method is not only robust to noise, but can also identify both partial and global symmetries. Moreover, we demonstrate the utility of our detected symmetries in various downstream tasks, such as compression and symmetrization of noisy shapes.

Method

The general idea of symmetry detection is to find a hyper-plane \((\textbf{n}, \textbf{p})\) that defines a reflection applicable to a significant part of the shape. Mitra et al. [2006] propose a "voting" approach with mean-shift clustering, where they observe that these votes create a density function in the transformation space. The modes of the density function then correspond to significant symmetries since they are a transformation that is proximal to most votes. In other words, symmetry detection can be formulated as a mode seeking procedure of the density defined in the transformation space. As robust mode seeking algorithms are well-studied in generative modeling, we introduce one, specifically Langevin dynamics, to symmetry detection. We establish a connection between Langevin dynamics and mean-shift algorithm used in symmetry detection and show that the introduction of Langevin dynamics helps improve robustness to noise while allowing us to detect both partial and global symmetries.
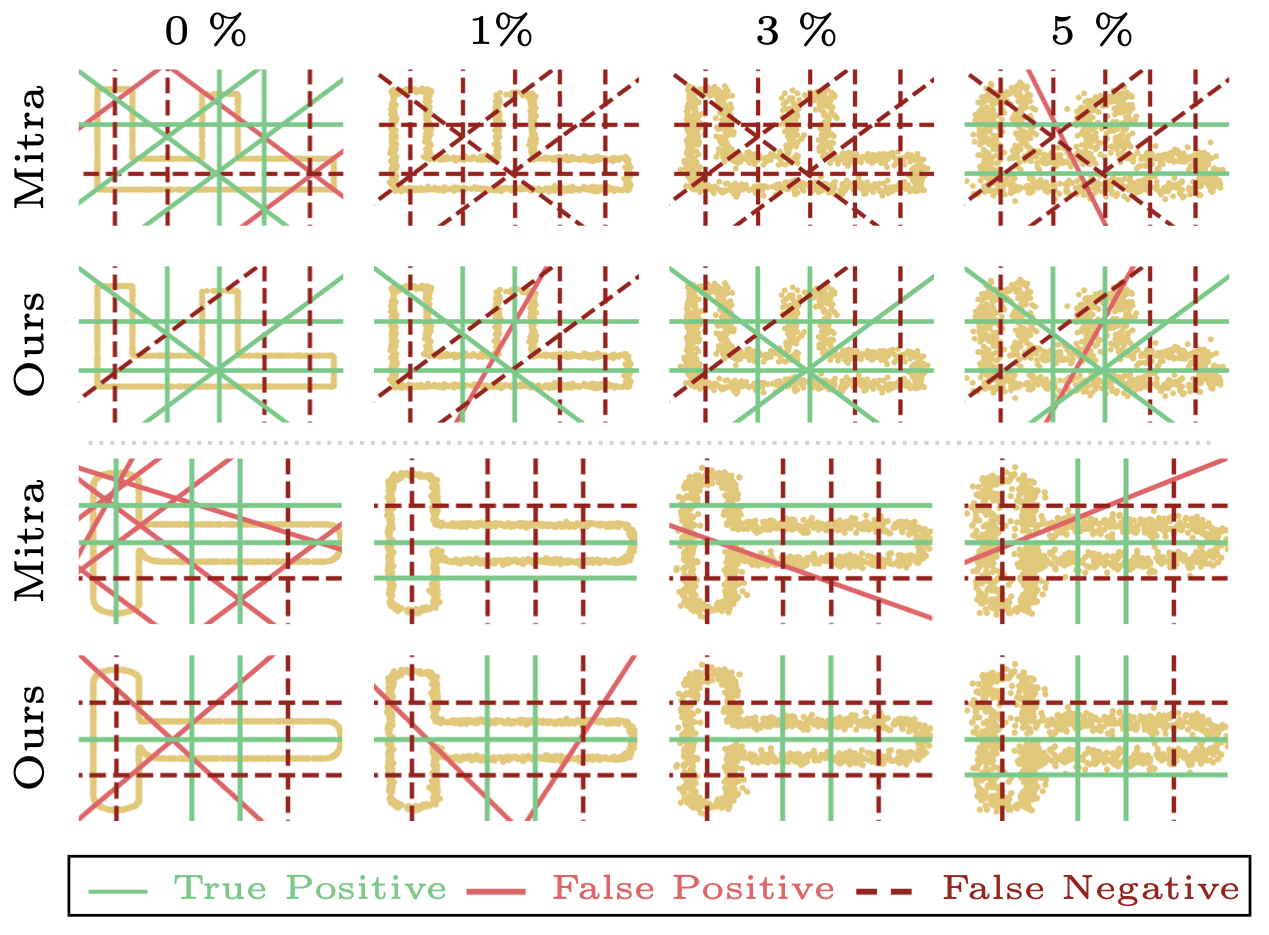
Symmetry Detection GIF
Transformation space construction. Every transformation for point-pair gets mapped to a point in the symmetry space.
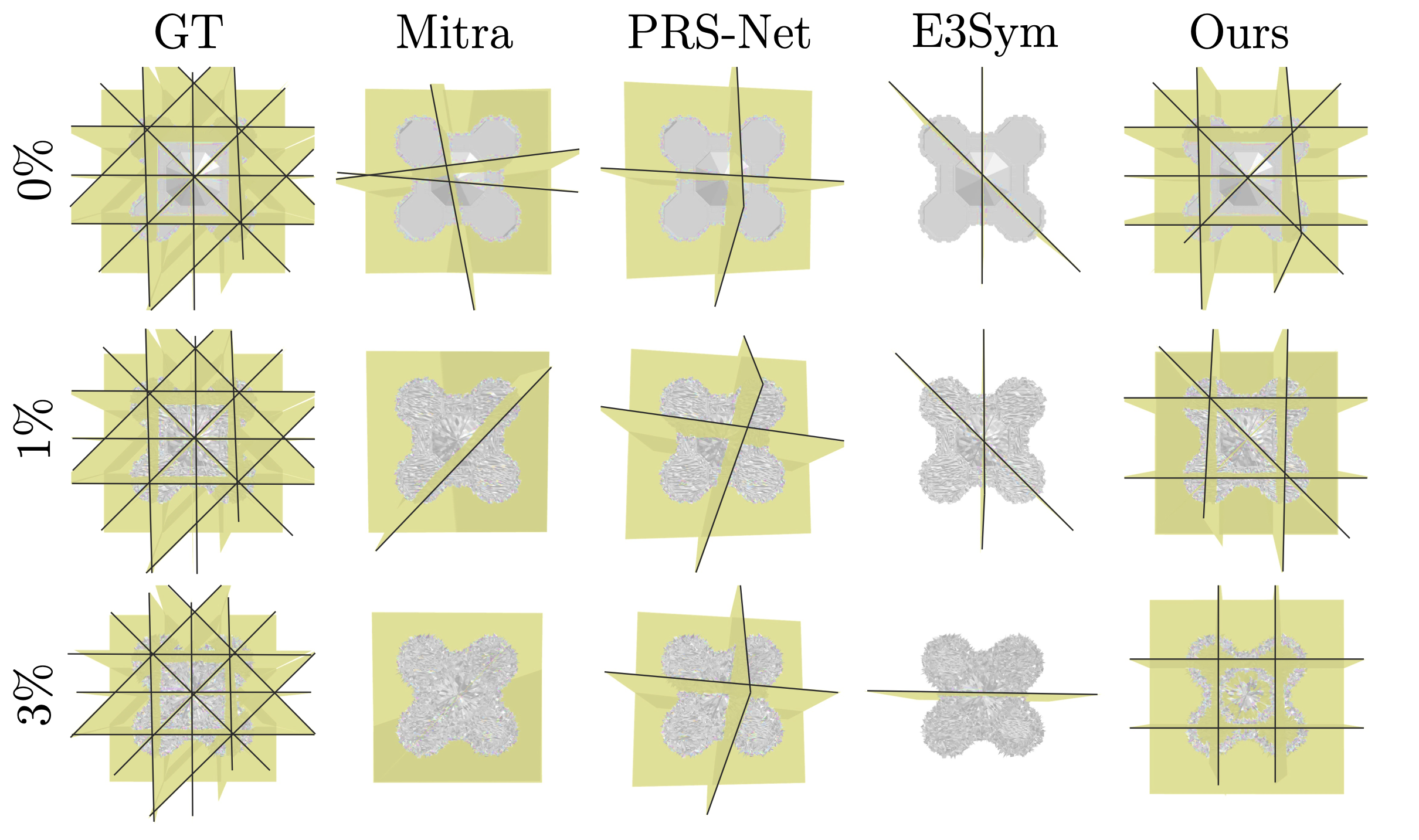
Symmetry Detection Image
Geodesic distance to the black point in transformation space. Blue indicates proximity, and red indicates larger distance. Shortest distance can be computed traveling through the origin as well.
One challenge of performing the walk in the transformation space defined as \(T(\textbf{p},\textbf{q})\) is that Euclidean distance in the space does not reflect the actual distance between symmetry plane. This is due to the fact that reflective symmetry contains \(SO(n)\) rotation symmetry. Fortunately, the score function can be computed in a Riemannian manifold where only distances are defined. In addition, we redefine a reflective symmetry manifold to directly walk on, derived from Hough-transform representation of hyperplanes. We hypothesize that the combined effects of such a transformation representation with the introduction Langevin dynamics improve robustness to noise.
Symmetry Detection GIF
Symmetry Detection Image
Visualizing Langevin dynamics trajectory. For each converged mode, we show the full trajectory (top row), as well as the corresponding symmetry in the shape space (bottom row). Note that due to our Langevin construction, we directly jump across the invalid region as opposed to stepping within it. When converged modes are near the boundary of the invalid region \((l \approx k)\), we see oscillations through the origin as the two modes are equivalent (\(H(0, \textbf{n}) = H(0, -\textbf{n}))\).

Results

Below, we provide empirical results on a variety of shapes that suggest our method is not only robust to noise, but can also identify both partial and global symmetries. Please see our full paper for more results and applications.
Symmetry Detection GIF
Qualitative results for 3D. We visualize the input 3D shape and selected reflective planes from our detection results. We only highlight the largest connected region that agrees to the symmetry, and color each side of the reflective plane differently. Results indicate that our method is capable of detecting symmetries of varying scales on a wide array of shapes.

Symmetry Detection GIF
Qualitative comparison with Mitra et al. [2006] for 2D. We visualize the input 2D font shapes and the predicted reflective symmetries for varying levels of noise. We show that our solution is more robust to noise, capable of detecting key symmetries even at high levels of noise.
Symmetry Detection Image


Qualitative comparison with baselines for 3D. All detected symmetries are shown for 0, 1, 3% noise. Our method is capable of detecting both local and global symmetries accurately even at high noise levels.

Acknowledgements

This work was supported by ARL grant W911NF-21-2-0104, Vannevar Bush Faculty Fellowship, and Azrieli Foundation Early Career Faculty Fellowship. We would also like to thank Eric Chan, Marcel Rød, Lucia Zheng, Chenglei Si, Zoe Wefers, George Nakayama, and Maolin Gao for all the helpful discussions and feedback.

BibTeX


@inproceedings{10.1145/3680528.3687682,
author = {Je, Jihyeon and Liu, Jiayi and Yang, Guandao and Deng, Boyang and Cai, Shengqu and Wetzstein, Gordon and Litany, Or and Guibas, Leonidas},
title = {Robust Symmetry Detection via Riemannian Langevin Dynamics},
year = {2024},
isbn = {9798400711312},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA},
url = {https://doi.org/10.1145/3680528.3687682},
doi = {10.1145/3680528.3687682},
booktitle = {SIGGRAPH Asia 2024 Conference Papers},
articleno = {91},
numpages = {11},
keywords = {Geometry Processing, Generative Modeling, Langevin Dynamics},
location = {Tokyo, Japan},
series = {SA '24}
}